# 搜索
# BFS⭐
广度优先搜索 一层一层地进行遍历,每层遍历都是以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
下面第一题的解题思路基本是模板:
# 1091. 二进制矩阵中的最短路径 (opens new window)
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, ..., C_k 组成:
- 相邻单元格
C_i和C_{i+1}在八个方向之一上连通(此时,C_i和C_{i+1}不同且共享边或角) C_1位于(0, 0)(即,值为grid[0][0])C_k位于(N-1, N-1)(即,值为grid[N-1][N-1])- 如果
C_i位于(r, c),则grid[r][c]为空(即,grid[r][c] == 0)
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。
示例 1:
输入:[[0,1],[1,0]]
输出:2
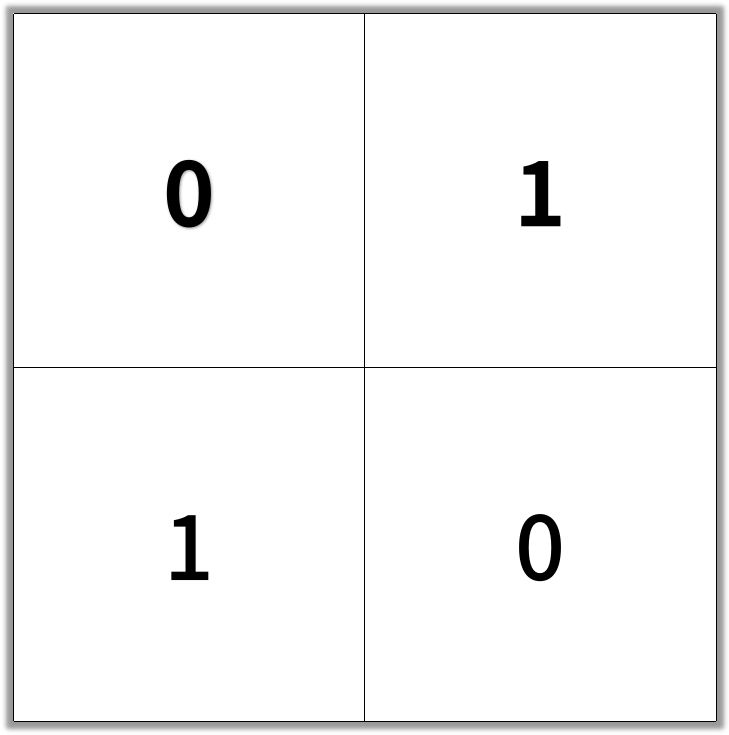
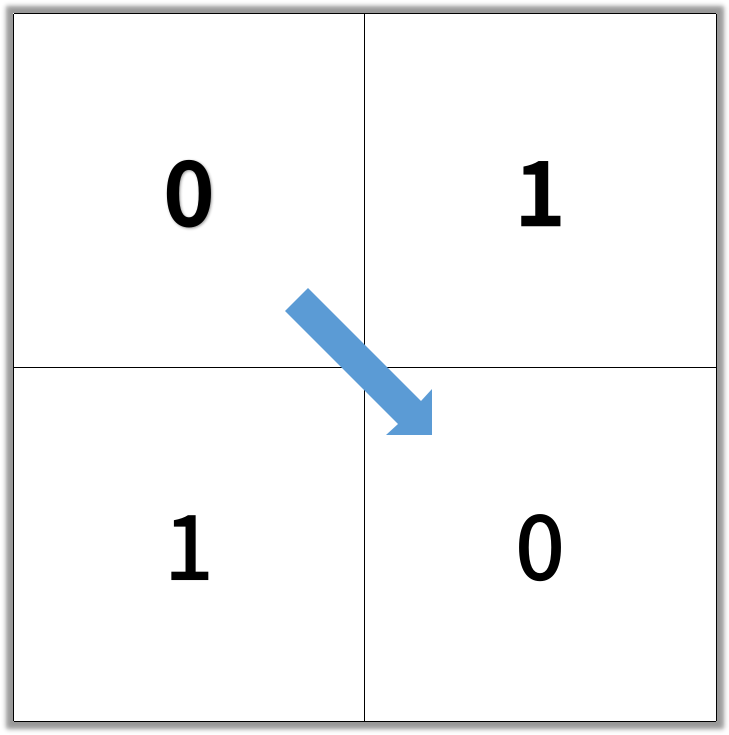
示例 2:
输入:[[0,0,0],[1,1,0],[1,1,0]]
输出:4
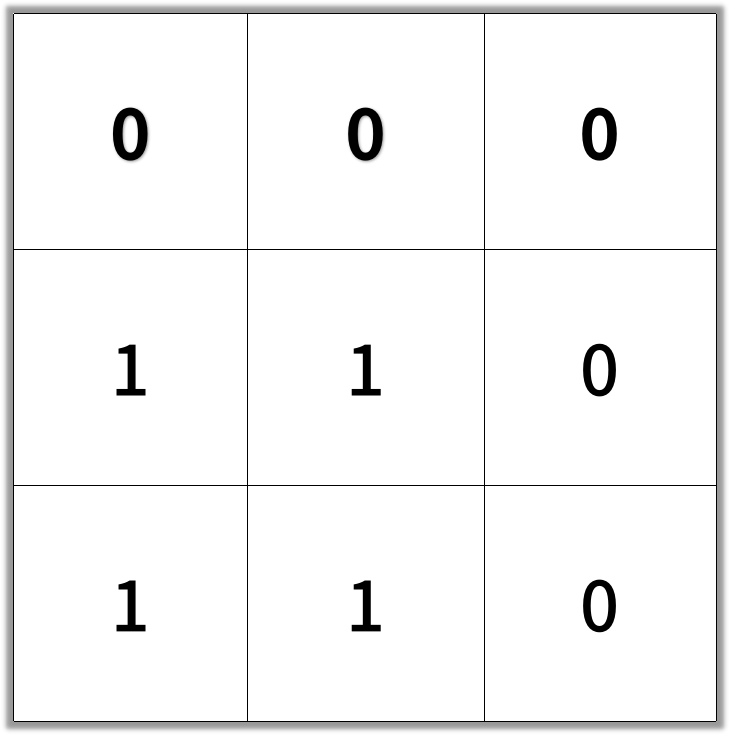
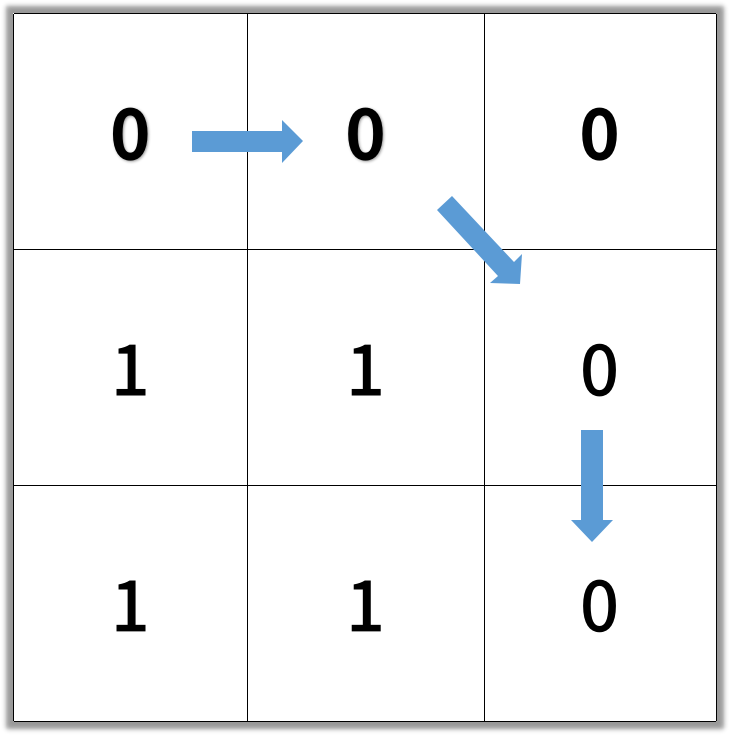
提示:
1 <= grid.length == grid[0].length <= 100grid[i][j]为0或1
题解:
排除特殊阻塞情况
把初始值压入队列 list
找出和搜索值距离相等的八个方向
findArrs三层循环:
- 判断 list 是否空了,空了还没 return 说明没结果
- 当前需要搜索的几个目标是否搜索完了,因为 list 在后面会被反复添加,所以在开始处用 i 记录一下长度作为循环依据
- 循环八个方向
pass 掉越界&已经标记过的&不符合要求的
标记这个位置为已遍历
塞入队列,作为下次循环需要循环的值
因为这八个方向不管有多少个为 0 的位置,他们都只能取一个,也就是 res++
/**
* @param {number[][]} grid
* @return {number}
*/
var shortestPathBinaryMatrix = function (grid) {
let res = 1
let k = grid.length - 1
// 开头结尾阻塞情况
if (grid[0][0] == 1 || grid[k][k] == 1) return -1
// 长度为1情况
if (grid.length == 1) return 1
let list = [[0, 0]]// 存储遍历值,初始值为第一个
let findArrs = [[-1, -1], [0, -1], [1, -1], [-1, 0], [1, 0], [-1, 1], [0, 1], [1, 1]]
let loopX, loopY
// 记得把初始值标记
grid[0][0] = 1
// 判断队列里是否还有待循环的
while (list.length != 0) {
let len = list.length
// 放在下面的while前面,一定会有一个下一层的值,先加上
res++
// 这个while必须用len来判断,因为list的内容在不断插入,而我们一轮只需要遍历开始插入前的那几个位置就行
while (len--) {
let [x, y] = list.shift()
for (let item of findArrs) {
loopX = x + item[0]
loopY = y + item[1]
// 如果到达了终点 返回res【前面res已经加过了】
if (x == k && y == k) return res
// 判断越界或者为1
if (loopX > k || loopY > k || loopX < 0 || loopY < 0 || grid[loopX][loopY] == 1) continue;
// 把这个位置标记为已遍历
grid[loopX][loopY] = 1
// 塞进队列
list.push([loopX, loopY])
}
}
}
return -1
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 279. 完全平方数 (opens new window)
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
2
3
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
2
3
题解:
这里的思路:
- 每一层用当前值循环减去从1开始的平方数,减下来的值 temp 如果是 0 ,说明已经结束
- 如果不为 0 ,说明还需要再减平方数,所以把这些 temp 塞进 queue
- 但是注意,如果这个 temp 已经访问过,那么再遇到的时候就不要访问了,因为那时候肯定不是最短路径
比如 13 ,在 13-1*1-2*2=8,这是第三层遇到了8,然后在 13-2*2-1*1=8 又遇到了8,这种重复值层数越高就可能越多,所以用 visited 去重。
也有可能是你在第三层碰到的值,我在第二层已经扔进过 queue 处理过了。
为什么用 level 来决定结果?
因为每减一次,不管你减多少,都肯定减去了一个平方数,level 就是减了几次平方数的次数。
下图每两个 step 中间就相当于我们的 level,step2 的 3 是 7-4 ,图上画错了
/**
* @param {number} n
* @return {number}
*/
var numSquares = function (n) {
let level = 0
let queue = [n] // 存放待处理值
let visited = new Set([n]) // 存放已经计算过的值
while (queue.length !== 0) {
level++
let len = queue.length
while (len--) {
let now = queue.shift()
for (let i = 1; i ** 2 <= now; i++) {
let temp = now - i ** 2
if (temp === 0) {
return level
}
if (!visited.has(temp)) {
visited.add(temp)
queue.push(temp)
}
}
}
}
return level
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 127. 单词接龙 (opens new window)
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。 - 序列中最后一个单词是
endWord。 - 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
2
3
题解1:
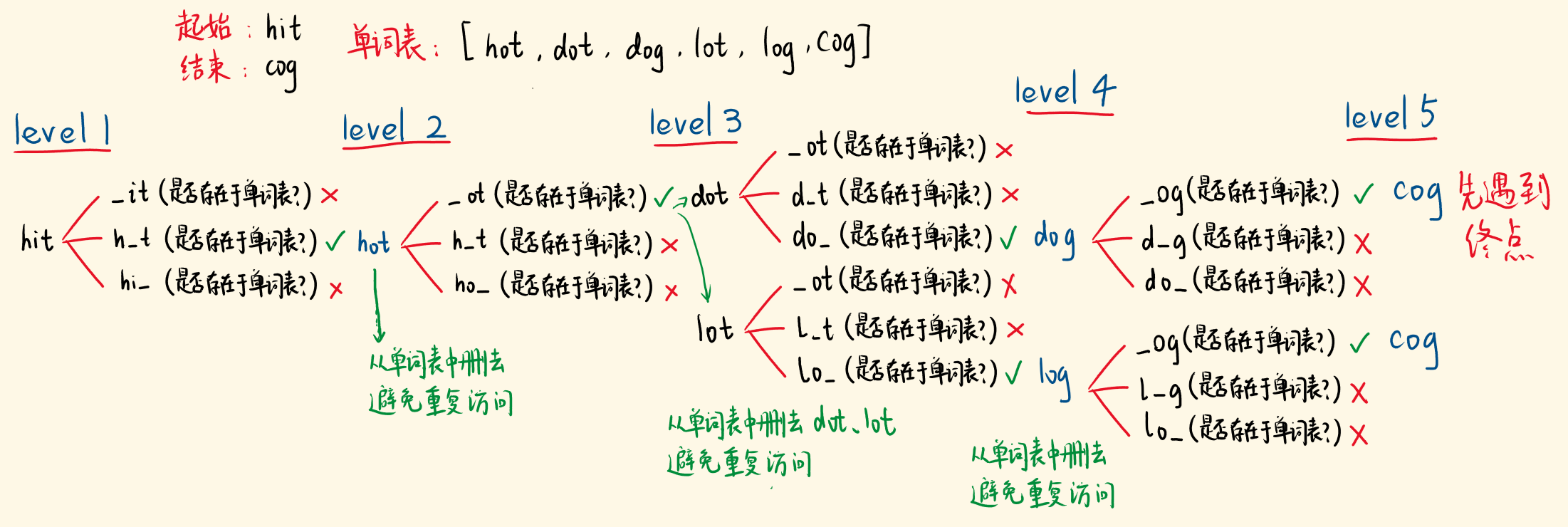
注意点:
- 用26个字母循环拼接字符串然后反过来查找 wordSet 是否存在目标字符,比每次循环 wordSet 效率高很多(wordSet 数量多)
- 本题标记的方法是塞入 queue 之后直接从 wordSet 中删除
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {number}
*/
var ladderLength = function (beginWord, endWord, wordList) {
let wordSet = new Set(wordList)
let queue = [beginWord]
let res = 0
if (!wordSet.has(endWord)) return 0
while (queue.length !== 0) {
let len = queue.length
res++
while (len--) {
let word = queue.shift()
if (word === endWord) return res
for (let i = 0; i < word.length; i++) {
for (let c = 97; c <= 122; c++) {
const newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1);
if (wordSet.has(newWord)) {
queue.push(newWord)
wordSet.delete(newWord)
}
}
}
}
}
return 0
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
题解2:
双向广度解法:我们可以从 beginWord 和 endWord 前后同时出发,进行 bfs,每一次循环并不是同时扩散双向队列,而是选择其中一个较小的队列进行扩散(扩散的波纹类似双指针),beforeQueue 始终是较小者(互换)
beforeQueue 中衍生出的 newWord 如果在 endQueue 中存在,则表示两者相遇;不需要判断 newWord 是否在 wordList 中,因为 endQueue 中存在的单词必定在 wordList 中
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {number}
*/
var ladderLength = function (beginWord, endWord, wordList) {
if (!wordList.includes(endWord)) { return 0 }
let beforeQueue = [[beginWord, 1]] // 从起点出发
let endQueue = [[endWord, 1]] // 从终点出发
const wordListSet = new Set(wordList)
while (beforeQueue.length && endQueue.length) { // 只有两者都不为空时,循环才继续,如果有一者为空,表示某一边已经走死,不能继续
if (beforeQueue.length > endQueue.length) {
[beforeQueue, endQueue] = [endQueue, beforeQueue] // beforeQueue始终保持较小
}
const currentLevelSize = beforeQueue.length
for (let i = 0; i < currentLevelSize; i++) {
const [word, level] = beforeQueue.shift()
for (let l = 0; l < word.length; l++) { // 遍历单词,把能转换的单词push入队列
for (let charCode = 97; charCode <= 122; charCode++) {
const newWord = `${word.slice(0, l)}${String.fromCharCode(charCode)}${word.slice(l + 1)}`
const index = endQueue.findIndex(item => item[0] === newWord)
if (index !== -1) { // 这里不需要判断newWord是否在wordList中,因为endQueue中存在的单词必定在wordList中
return endQueue[index][1] + level
}
if (wordListSet.has(newWord)) {
beforeQueue.push([newWord, level + 1])
wordListSet.delete(newWord)
}
}
}
}
}
return 0
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
整体变化如下:
* 代表被 shift() 或者 delete()
相当于一条线找出了 "hit" -> "hot" -> "dot" -> "dog" 这条线,另外一条找出了 "cog" -> "dog" 这条线
"hit","cog",["hot","dot","dog","lot","log","cog"]
------------------------------------------------
level:1 begin hit
level:1 end cog
["hot","dot","dog","lot","log","cog"]
------------------------------------------------
level:2 begin *hit hot
level:1 end cog
[*"hot","dot","dog","lot","log","cog"]
------------------------------------------------
level:3 begin *hit *hot dot lot
level:1 end cog
[*"dot","dog",*"lot","log","cog"]
------------------------------------------------
level:3 end *hit *hot dot lot
level:2 begin *cog dog log cog
[*"dog",*"log",*"cog"]
------------------------------------------------
level:3 begin *hit *hot 【dot】 lot
level:2 end *cog 【dog】 log cog
[]
【dot】变化出【dog】在 end 中命中!
return 3 + 2 = 5
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 有向图的拓扑排序和卡恩算法
拓扑排序的定义: 在计算机科学领域,有向图的拓扑排序或拓扑测序是对其顶点的一种线性排序,使得对于从顶点u到顶点v的每个有向边uv,u在排序中都在v之前。
例如,图形的顶点可以表示要执行的任务,并且边可以表示一个任务必须在另一个任务之前执行的约束;在这个应用中,拓扑排序只是一个有效的任务顺序。 当且仅当图中没有定向环时(即有向无环图),才有可能进行拓扑排序。 任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内,构建任何有向无环图的拓扑排序。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,才能称为该图的一个拓扑排序(英语:Topological sorting):
1.序列中包含每个顶点,且每个顶点只出现一次;
2.若A在序列中排在B的前面,则在图中不存在从B到A的路径。
卡恩算法很精准地说明了BFS的精髓
L ← 包含已排序的元素的列表,目前为空
S ← 入度为零的节点的集合
当 S 非空时:
将节点n从S移走
将n加到L尾部
选出任意起点为n的边e = (n,m),移除e。如m没有其它入边,则将m加入S。
重复上一步。
如图中有剩余的边则:
return error (图中至少有一个环)
否则:
return L (L为图的拓扑排序)
2
3
4
5
6
7
8
9
10
11
维基百科: Link (opens new window)
# 207. 课程表 (opens new window)
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
2
3
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
2
3
题解
以 [[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]] 为例子, [3,0] 就是以0为出度,3为入度,构建了一条0-3的有向边,将所有构建起来是这些的,借用一下这个题解 (opens new window)的图片:

分析结构我们可以构建如下的数据结构:
in: 入度值 out: 出度值 deps: 依赖项
0:{in:0,out:1,deps:[3]}
1:{in:0,out:2,deps:[3,4]}
2:{in:0,out:1,deps:[4]}
3:{in:2,out:1,deps:[5]}
4:{in:2,out:1,deps:[5]}
5:{in:2,out:0,deps:[]}
2
3
4
5
6
7
我们先取出所有入度为0的塞入队列,因为不会有人指向他们为边,当我们处理0的时候,等于也处理了0-3这条有向边,此时3的入度就会-1,当一个值的入度被处理到0的时候,就可以塞入队列,直到所有可以处理的值的入度都是0(队列为空),此时如果还有多的值,那么一定是存在至少一个环
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {boolean}
*/
var canFinish = function (numCourses, prerequisites) {
let queue = []
// in: 入度值 out: 出度值 deps: 依赖项
let map = new Map([...Array(numCourses).keys()].map(item => ([item, { in: 0, out: 0, deps: new Set() }])))
// 计算入度 出度 和依赖当前值的值列表
for (let i = 0; i < prerequisites.length; i++) {
map.get(prerequisites[i][0]).in++
map.get(prerequisites[i][1]).out++
map.get(prerequisites[i][1]).deps.add(prerequisites[i][0])
}
// 找出入度为0的值
for (let [key, value] of map.entries()) {
if (value.in === 0) {
queue.push(key)
}
}
// 类似BFS
let count = 0
while (queue.length > 0) {
// 遍历queue pop一个就代表把以这个值为出度的有向边去除 把对应的deps的入度减1
const outNum = queue.pop()
count++
for (let item of map.get(outNum).deps) {
if (--(map.get(item).in) === 0) {
queue.push(item)
}
}
}
return count === numCourses
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 210. 课程表 II (opens new window)
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组
题解
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {number[]}
*/
var findOrder = function (numCourses, prerequisites) {
let queue = []
// in: 入度值 out: 出度值 deps: 依赖项
let map = new Map([...Array(numCourses).keys()].map(item => ([item, { in: 0, out: 0, deps: new Set() }])))
// 计算入度 出度 和依赖当前值的值列表
for (let i = 0; i < prerequisites.length; i++) {
map.get(prerequisites[i][0]).in++
map.get(prerequisites[i][1]).out++
map.get(prerequisites[i][1]).deps.add(prerequisites[i][0])
}
// 找出入度为0的值
for (let [key, value] of map.entries()) {
if (value.in === 0) {
queue.push(key)
}
}
// 类似BFS
let res = [], count = 0
while (queue.length > 0) {
// 遍历queue pop一个就代表把以这个值为出度的有向边去除 把对应的deps的入度减1
const outNum = queue.pop()
res.push(outNum)
count++
for (let item of map.get(outNum).deps) {
if (--(map.get(item).in) === 0) {
queue.push(item)
}
}
}
return count === numCourses ? res : []
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# DFS⭐
DFS(深度优先搜索) 是先每次都沿着可能的一条线一直搜索到 边缘或者不满足条件为止
从一个节点出发,使用 DFS 对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS 常用来求解这种 可达性 问题。
在程序实现 DFS 时需要考虑以下问题:
- 栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
- 标记:和 BFS 一样同样需要对已经遍历过的节点进行标记。
# 695. 岛屿的最大面积 (opens new window)
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
2
3
4
5
6
7
8
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
示例 2:
[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。
题解:
/**
* @param {number[][]} grid
* @return {number}
*/
var maxAreaOfIsland = function (grid) {
let ans = 0
let x = grid.length
let y = grid[0].length
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (grid[i][j] === 0) continue;
ans = Math.max(ans, sub(i, j, grid))
}
}
return ans
};
function sub(i, j, grid) {
let x = grid.length
let y = grid[0].length
// 判断边界
if (i < 0 || i >= x || j < 0 || j >= y || grid[i][j] === 0) return 0
let count = 1
grid[i][j] = 0
// 定义四个方向
let directions = [[0, -1], [0, 1], [-1, 0], [1, 0]]
// 是陆地的话,查看每个方向是不是陆地
for (let dir of directions) {
let [loopX, loopY] = [i + dir[0], j + dir[1]]
// 递归
count += sub(loopX, loopY, grid)
}
return count
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 200. 岛屿数量 (opens new window)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 :
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
2
3
4
5
6
7
题解:
/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function (grid) {
let ans = 0
let x = grid.length, y = grid[0].length
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (grid[i][j] == "1") {
sub(i, j, grid)
ans++
}
}
}
return ans
};
function sub(i, j, grid) {
let x = grid.length, y = grid[0].length
if (i < 0 || i >= x || j < 0 || j >= y || grid[i][j] == "0") return
grid[i][j] = "0"
sub(i - 1, j, grid)
sub(i + 1, j, grid)
sub(i, j - 1, grid)
sub(i, j + 1, grid)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 547. 省份数量 (opens new window)
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:

输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
2
题解:
/**
* @param {number[][]} isConnected
* @return {number}
*/
var findCircleNum = function (isConnected) {
let x = isConnected.length
let ans = 0
for (let i = 0; i < x; i++) {
/**
* 判断代表这个城市自身的 isConnected[i][i] 是否为 1
* 这个值初始的时候一定为1,因为城市肯定和自身链接
* 为 1 说明我们走过这层城市了,用这个方法来标记是否访问过
* */
if (isConnected[i][i] == 1) {
ans++
dfs(i, isConnected, x)
}
}
return ans
};
function dfs(i, isConnected, x) {
// 遍历这个城市的关联情况
for (let j = 0; j < x; j++) {
if (isConnected[i][j] == 1) {
if (i == j) {
// 来到新的城市要把城市自身标识为0,代表我们访问过
isConnected[i][j] = 0
} else {
// 和别的城市关联,把相关联的都置0
isConnected[i][j] = 0
isConnected[j][i] = 0
// 开始遍历关联的那个城市
dfs(j, isConnected, x)
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 130. 被围绕的区域 (opens new window)
给定一个二维的矩阵,包含 'X' 和 'O'(字母 O)。
找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例:
X X X X
X O O X
X X O X
X O X X
2
3
4
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
2
3
4
解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
题解:
思路:
由于任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。所以我们先在边界上找到所有的 '0' ,然后从他们开始做 DFS
把这些标记为其他字符,注意不能弄个 set 或者数组存 [i,j] 这样的,数组是引用类型,后面你就不好找了。
最后遍历整个矩阵判断就好。
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
var solve = function (board) {
if (!board.length) return
let x = board.length, y = board[0].length
// 查找边框上的 O
// top bottom
for (let i = 0; i < y; i++) {
if (board[0][i] == 'O') { dfs(0, i, board) }
if (board[x - 1][i] == 'O') { dfs(x - 1, i, board) }
}
// left right
for (let i = 0; i < x; i++) {
if (board[i][0] == 'O') { dfs(i, 0, board) }
if (board[i][y - 1] == 'O') { dfs(i, y - 1, board) }
}
// loop all
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X'
}
if (board[i][j] == '@') {
board[i][j] = 'O'
}
}
}
};
function dfs(i, j, board) {
let x = board.length, y = board[0].length
if (i < 0 || i >= x || j < 0 || j >= y || board[i][j] !== 'O') return
if (board[i][j] == 'O') {
board[i][j] = '@'
dfs(i - 1, j, board)
dfs(i + 1, j, board)
dfs(i, j - 1, board)
dfs(i, j + 1, board)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 417. 太平洋大西洋水流问题⭐ (opens new window)
给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。
规定水流只能按照上、下、左、右四个方向流动,且只能从高到低或者在同等高度上流动。
请找出那些水流既可以流动到“太平洋”,又能流动到“大西洋”的陆地单元的坐标。
提示:
- 输出坐标的顺序不重要
- m 和 n 都小于150
示例:
给定下面的 5x5 矩阵:
太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * 大西洋
返回:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).
2
3
4
5
6
7
8
9
10
11
12
13
题解:
思路:
- 反向思考,从边界向内靠拢,和 130. 被围绕的区域 思路很像
- 但是注意,我们只需要在意每个海洋能辐射到的总范围就行,不需要在意最远是哪些个值(一开始思路走的这个,发现边缘判断很麻烦)
- 最后取两个海洋的辐射范围交集就行
Tips:这里创建二维数组的方式很好用:
Array.from({length: x}, () => new Array(y).fill(xxx));
亲测发现比 new Array -> map(new Array) 的方式快很多!
/**
* @param {number[][]} matrix
* @return {number[][]}
*/
var pacificAtlantic = function (matrix) {
if (matrix.length == 0) return []
let ans = []
let x = matrix.length
let y = matrix[0].length
let daxi = Array.from({length: x}, () => new Array(y).fill(false));
let taiping = Array.from({length: x}, () => new Array(y).fill(false));
//top bottom
for (let i = 0; i < y; i++) {
dfs(0, i, matrix, taiping)
dfs(x - 1, i, matrix, daxi)
}
//left right
for (let i = 0; i < x; i++) {
dfs(i, 0, matrix, taiping)
dfs(i, y - 1, matrix, daxi)
}
// 比较两个数组的相同值
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (taiping[i][j] && taiping[i][j] == daxi[i][j]) {
ans.push([i, j])
}
}
}
return ans
};
function dfs(i, j, matrix, arr) {
/**
* 四个方向的值
* 如果已经走过了(true)、越界了、比当前值小,都不用再dfs
* 否则,赋值true
* dfs
*/
let x = matrix.length, y = matrix[0].length
let dirs = [[0, 1], [0, -1], [-1, 0], [1, 0]]
if (arr[i][j]) return
arr[i][j] = true
for (let dir of dirs) {
let loopx = i + dir[0]
let loopy = j + dir[1]
if (loopx < 0 || loopx >= x || loopy < 0 || loopy >= y || matrix[i][j] > matrix[loopx][loopy]) continue
dfs(loopx, loopy, matrix, arr)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# Backtracking⭐
Backtracking(回溯)属于 DFS。
- 普通 DFS 主要用在 可达性问题 ,这种问题只需要执行到特点的位置然后返回即可。
- 而 Backtracking 主要用于求解 排列组合 问题,例如有 { 'a','b','c' } 三个字符,求解所有由这三个字符排列得到的字符串,这种问题在执行到特定的位置返回之后还会继续执行求解过程。
# 17. 电话号码的字母组合 (opens new window)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
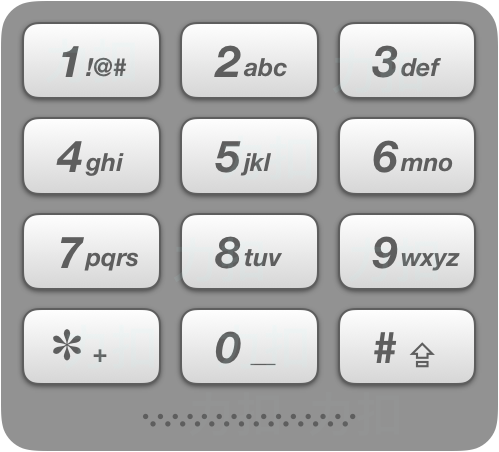
示例 1:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = "" 输出:[]
示例 3:
输入:digits = "2" 输出:["a","b","c"]
提示:
0 <= digits.length <= 4 digits[i] 是范围 ['2', '9'] 的一个数字。
题解:
思路:
每次传入的参数是当前字母的下标,和递归到当前为止拼出来的字符串(是把整个字符串作为参数传进去)
当这个字符串拼接到当前下标越界就说明拼完了,填入 ans
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function (digits) {
if (!digits.length) return []
let ans = []
let numChar = new Map([
["2", ["a", "b", "c"]], ["3", ["d", "e", "f"]],
["4", ["g", "h", "i"]], ["5", ["j", "k", "l"]], ["6", ["m", "n", "o"]],
["7", ["p", "q", "r", "s"]], ["8", ["t", "u", "v"]], ["9", ["w", "x", "y", "z"]],
])
dfs("", 0)
/**
* @description:
* @Author: rodrick
* @Date: 2021-02-01 08:52:57
* @param {*} char 当前字母组合
* @param {*} index 数字下标
* @return {*}
*/
function dfs(char, index) {
if (index > digits.length - 1) {
ans.push(char)
return
}
// 获取 要遍历的字母
const chars = numChar.get(digits[index])
// 遍历每一个字母,然后让他们都去和后面的每一个数字去对接
for (let c of chars) {
dfs(char + c, index + 1)
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 93. 复原IP地址 (opens new window)
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.'分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
2
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
2
题解:
这题的关键:
捋清楚关系树下哪些情况是不要的情况,这些情况我们得“减枝,借用一张图说明一下,来源是这里 (opens new window)
- 首位是0,但长度非1
- 剩余位数过长或者过短
- 出范围 [0,255]
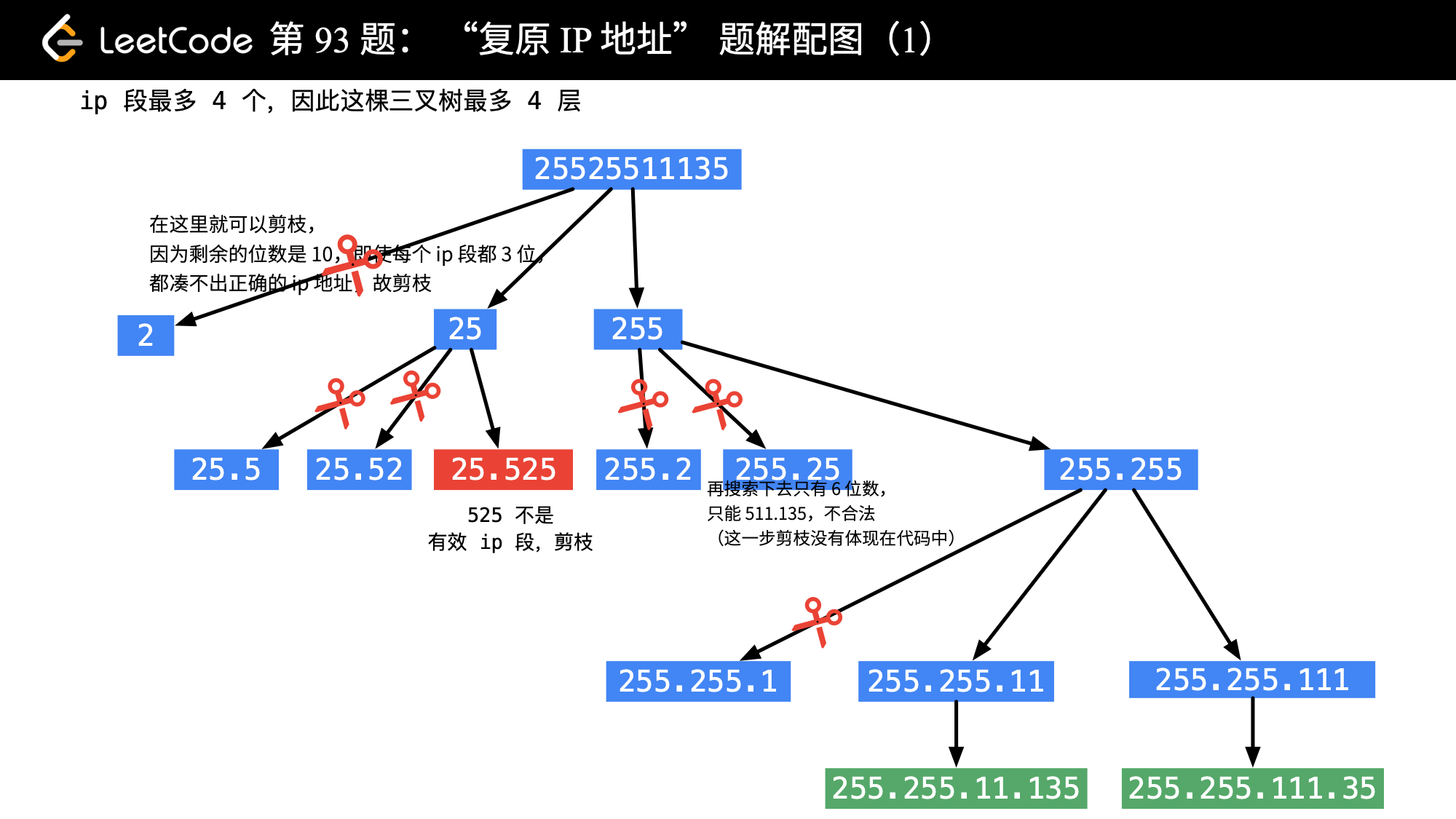
- ⭐我们每次传的是数组,和17题不同,数组作为引用类型,每次循环中引用的都是堆中同一个数组,所以我们在
push后传入递归后,需要把刚才传入的值给pop()
/**
* @param {string} s
* @return {string[]}
*/
var restoreIpAddresses = function (s) {
let ans = []
dfs([], 0)
// 传入拼接到目前的ipstr和下标
function dfs(ip, i) {
const ipLen = ip.length
// 如果ip段数==4且下标==长度说明正好遍历结束
if (ipLen == 4 && i == s.length) {
ans.push(ip.join('.'))
return
}
// 如果下标越界或者已经四段了但是下标没结束,就结束
if (i >= s.length || (ipLen == 4 && i < s.length)) return
//开始截取
let len = 0
while (len++ < 3) {
const temp = s.substr(i, len)
/**
* 这些情况需要放弃这次回溯:
* 首位是0,但长度非1
* 剩余位数过长或者过短
* 超出范围
*/
if ((temp[0] == "0" && temp.length != 1)
|| (s.length - (i + len) > (4 - (ipLen + 1)) * 3)
|| (s.length - (i + len) < (4 - (ipLen + 1)) * 1)
|| +temp > 255) continue
// 正常走下去
ip.push(temp)
dfs(ip, i + len)
// 【注意!】每次传完之后,这个ip数组需要把刚才加进去的给减掉,
// 不然的话继续循环或者递归这个数组里的值就越来越多了,他们都是引用堆里同一个数组对象ip
ip.pop()
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 79. 单词搜索 (opens new window)
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
2
3
4
5
6
7
8
9
10
提示:
board和word中只包含大写和小写英文字母。1 <= board.length <= 2001 <= board[i].length <= 2001 <= word.length <= 10^3
题解:
典型回溯,记录已经走过的二维数组位置的方法很经典,其他就是套路:判断越界+判断错误值+判断是否走过
然后递归 dfs ,只要有一个成功就返回 true
/**
* @param {character[][]} board
* @param {string} word
* @return {boolean}
*/
var exist = function (board, word) {
let x = board.length, y = board[0].length
let list = Array.from({ length: x }, () => new Array(y).fill(false))
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (board[i][j] === word[0]) {
if (dfs(0, i, j)) {
return true
}
}
}
}
return false
// 拼接的字符串,当前字符串位置的下标,当前最后一个字母坐标
function dfs(i, locx, locy) {
let res = false
// 相等了直接返回true
if (i == word.length) return true
// 越界
if (locx < 0 || locx >= x || locy < 0 || locy >= y || i >= word.length) return false
// 值不等或者已经存在
if (board[locx][locy] != word[i] || list[locx][locy]) return false
// 值访问过标记
list[locx][locy] = true
// 上下左右dfs
let arr = [[0, 1], [0, -1], [1, 0], [-1, 0]]
for (let temp of arr) {
let loopx = locx + temp[0], loopy = locy + temp[1]
// dfs
let back = dfs(i + 1, loopx, loopy)
if (back) {
res = true
break;
}
}
list[locx][locy] = false
return res
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 257. 二叉树的所有路径 (opens new window)
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
2
3
4
5
6
7
8
9
10
11
题解:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {string[]}
*/
var binaryTreePaths = function (root) {
let ans = []
if (!root) return []
looptree(root, "")
// 当前树和上一层的值+"->"
function looptree(tree, str) {
// 保证传进来的 tree 为 true
str += tree.val.toString()
if (!tree.left && !tree.right) {
ans.push(str)
return
}
if (tree.left) {
looptree(tree.left, str + '->')
}
if (tree.right) {
looptree(tree.right, str + '->')
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 46. 全排列 (opens new window)
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
2
3
4
5
6
7
8
9
10
题解:
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function (nums) {
/**
* 唯一需要注意的是这里用了个use作为判断依据而不是用
* arr.includes(num)
* 是因为includes时间复杂度O(n),
* 用对象相当于我们用空间换时间
*/
let ans = []
let use = {}
dfs([])
function dfs(arr) {
if (arr.length == nums.length) {
ans.push(arr.slice(0))
}
for (let num of nums) {
if (!use[num]) {
arr.push(num)
use[num] = true
dfs(arr)
arr.pop()
use[num] = false
}
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
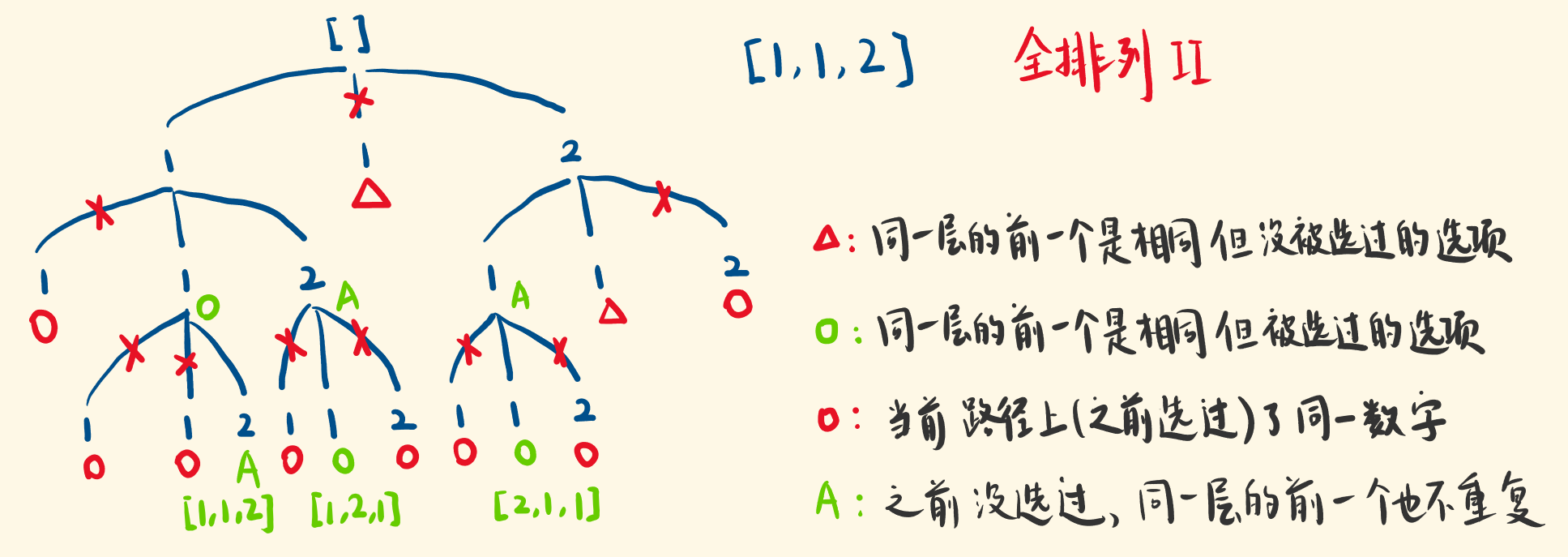
# 47. 全排列 II (opens new window)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
2
3
4
5
题解:
和上面一题不一样的关键点在于,nums 是有重复的,然后我们在选取的时候,需要“剪枝”,为了方便,我们必须要先进行==排序==,让相同的值放在一起
剪枝的方法主要是:
- 【A】如果上层用过了,pass
- 【B】前一个数和当前数相同且未被上层用过,那么前一个数要么已经被这轮选中,要么前N个相同数都因为同原因被pass
这样剪完之后剩下两种情况:
和前一个值相同但是前一个值上层用过,所以前一个值在【A】已经被pass,所以可用
和前一个值不同,且上层也没用过,所以可用
参考图解,来源 - LeetCode (opens new window)
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permuteUnique = function (nums) {
let ans = []
let use = new Map()
// 很关键的排序
nums.sort((a, b) => a - b)
dfs([])
function dfs(arr) {
// 长度相同就结束
if (arr.length == nums.length) {
ans.push(arr.slice())
return
}
for (let i in nums) {
// 【A】如果上层用过了,pass
if (use.get(i)) continue
// 【B】前一个数和当前数相同且未被上层用过,那么前一个数要么已经被这轮选中,要么前N个相同数都因为同原因被pass
// 注意,map的get的key是字符串
if (nums[i - 1] == nums[i] && !use.get(i - 1+"")) continue
// 剩下的情况就只有
// 1. 和前一个值相同但是前一个值上层用过,所以前一个值在【A】已经被pass,所以可用
// 2. 和前一个值不同,且上层也没用过,所以可用
use.set(i, true)
arr.push(nums[i])
dfs(arr)
arr.pop()
use.set(i, false)
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 77. 组合 (opens new window)
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
2
3
4
5
6
7
8
9
10
题解:
/**
* @param {number} n
* @param {number} k
* @return {number[][]}
*/
var combine = function (n, k) {
let ans = []
dfs([])
function dfs(arr) {
if (arr.length == k) {
ans.push(arr.slice())
return
}
let len = arr.length
// num 直接从数组最后一位数+1开始遍历,相当于前面的剪枝,因为后面的数一定大于前面并且都是+1关系
for (let num = arr.length ? arr[len - 1] + 1 : 1; num <= n; num++) {
// 当前数组+剩余数字长度不足时,直接结束循环,不用浪费时间遍历到最后才发现可用数字不够了
if (len + (n - num + 1) < k) {
break;
}
arr.push(num)
dfs(arr)
arr.pop()
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 39. 组合总和 (opens new window)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例 1:
输入:candidates = [2,6,3,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
2
3
4
5
6
题解:
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function (candidates, target) {
let ans = []
// 需要排序
candidates.sort((a, b) => a - b)
dfs([], 0, 0)
function dfs(arr, sum, index) {
// 相等了 push
if (sum == target) {
ans.push(arr.slice())
return
}
for (let i = index; i < candidates.length; i++) {
// 如果 sum+当前number>target,那么后续的循环都不用做了【前提条件是我们是排好序的】
if (sum + candidates[i] > target) {
break;
}
arr.push(candidates[i])
dfs(arr, sum + candidates[i], i)
arr.pop()
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 40. 组合总和 II (opens new window)
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。 解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
2
3
4
5
6
7
8
题解:
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function (candidates, target) {
candidates.sort((a, b) => a - b)
let ans = []
let use = new Map()
dfs([], 0, 0)
/**
* @description:
* @Author: rodrick
* @Date: 2021-02-06 22:10:09
* @param {*} arr 当前数组
* @param {*} sum 总和
* @param {*} index 下一位数的下标
*/
function dfs(arr, sum, index) {
if (sum == target) {
ans.push(arr.slice())
return
}
for (let i = index; i < candidates.length; i++) {
/** 如果前面一个数(i-1)被用过,那么当前的i肯定可以用,是新的组合
* 如果i的值和前面一个数(i-1)值一样且i-1没被用过,那么他(i-1)为什么没被用?
* 因为假设数组[1, 1, 1, 1], 其中index = 0的“1”是被用过的,那么index = 1的一定是可用的,【同层中】index > 1的如果再用就会产生重复结果
*/
if (candidates[i - 1] == candidates[i] && !use.get(i - 1)) continue;
// 如果加了这个值后比目标大,直接break结束循环
if (sum + candidates[i] > target) break;
use.set(i, true)
arr.push(candidates[i])
dfs(arr, sum + candidates[i], i + 1)
arr.pop()
use.set(i, false)
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 216. 组合总和 III (opens new window)
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。 解集不能包含重复的组合。
示例 1:
输入:
k = 3, n = 7
输出:
[[1,2,4]]
2
3
4
5
题解:
/**
* @param {number} k
* @param {number} n
* @return {number[][]}
*/
var combinationSum3 = function (k, n) {
let ans = []
dfs([], 1, 0)
function dfs(arr, num, sum) {
if (sum == n && arr.length == k) {
ans.push(arr.slice())
return
}
if (sum > n || num > 9 || arr.length >= k) {
return
}
for (let i = num; i <= 9; i++) {
arr.push(i)
dfs(arr, i + 1, sum + i)
arr.pop()
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 78. 子集 (opens new window)
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
2
题解:
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function (nums) {
let ans = []
dfs([], 0)
function dfs(arr, index) {
ans.push(arr.slice())
if (index > nums.length - 1) return
for (let i = index; i <= nums.length - 1; i++) {
arr.push(nums[i])
dfs(arr, i + 1)
arr.pop()
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 90. 子集 II (opens new window)
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
**说明:**解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
2
3
4
5
6
7
8
9
10
题解:
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function (nums) {
let ans = []
nums.sort((a, b) => a - b)
let use = new Set()
dfs([], 0)
function dfs(arr, index) {
ans.push(arr.slice())
for (let i = index; i <= nums.length - 1; i++) {
if (nums[i - 1] !== nums[i]
|| (nums[i - 1] === nums[i] && use.has(nums[i]))) {
use.add(nums[i])
arr.push(nums[i])
dfs(arr, i + 1)
use.delete(nums[i])
arr.pop()
}
}
}
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 131. 分割回文串 (opens new window)
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
2
3
4
5
6
题解:
思路:正常的回溯思路,在判断回文字符串的时候方式多样,我选择的是判断每次切割下来的字符串是否是回文
aab => 切下来 a,是回文 => 接下来切出来 a,是回文 => 接下来切出来 b,是回文 => 得到 [a,a,b]
=> index+1 切出来 ab 不是回文 continue => 数组切完结束,没有结果
=> index+1 切下来 aa 是回文 continue => 切出来 b 是回文,得到 [aa,b]
=> index+1 切下来 aab 不是回文 continue => 切完了,没有结果
2
3
4
/**
* @param {string} s
* @return {string[][]}
*/
var partition = function (s) {
let ans = []
dfs([], 0)
function dfs(arr, index) {
if (index === s.length) {
ans.push(arr.slice())
}
for (let i = index; i <= s.length-1; i++) {
const tempStr = s.substring(index, i + 1)
if (!isPal(tempStr)) continue;
arr.push(tempStr)
dfs(arr, i + 1)
arr.pop()
}
}
return ans
};
function isPal(s) {
let l = 0, r = s.length - 1
while (l < r) {
if (s[l] !== s[r]) return false
l++
r--
}
return true
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 37. 解数独 (opens new window)
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。
空白格用 '.' 表示。
题解:
思路:
- 判断是否冲突
- 行列是否有存在的值
- 所在 3x3 的格子里是否有存在的值
- 3x3 的格子起点只有 0 3 6 三种,用
Math.floor(x / 3) * 3计算
- 填数逻辑
- 先判断是否越界(行列超过 8 )
- 判断是否可填(等于
.),如果不可填那么直接递归下一个值【下一个值直接y+1,不用关心越界,因为步骤 1 进行了处理】 - 可填的情况下,循环 1-9:
- 先判断当前数是否冲突,冲突则 continue
- 不冲突的话填入,然后直接递归下一个值(
y+1)是否能构成数独,如果可以,直接返回true,不走步骤 3,这样保证board不会被修改。 - 如果步骤 2 的下一个值递归不能构成数独,那么把当前值重置为
.
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
const solveSudoku = (board) => {
fill(0, 0)
function fill(x, y) {
// 判断越界情况
// 如果列超出了就加行,如果行也超出去了说明填完了
if (y == 9) {
x++
y = 0
if (x == 9) return true
}
//判断是不是需要填的格子
if (board[x][y] !== '.') return fill(x, y + 1)
// 正常填
for (let num = 1; num <= 9; num++) {
// 如果有冲突 填写下一个数
if (hasConflit(x, y, num.toString())) continue
// 没冲突,填进去
board[x][y] = num.toString()
// 看看后面一个值可不可以做完数独,如果可以做完数独,则返回true,就没有改回”.“的机会了
if (fill(x, y + 1)) return true
// 不能完成数独,改回"." ,然后继续循环
board[x][y] = "."
}
// 如果循环完了九个数字都不能完成数独,那么才返回 false
return false
}
function hasConflit(x, y, num) {
// 判断行列是否有冲突
for (let i = 0; i <= 8; i++) {
if (board[x][i] === num || board[i][y] === num) return true
}
// 判断3x3的格子里有没有冲突
// 取所在3x3的格子的起点,起点只有 0 3 6
const inX = Math.floor(x / 3) * 3
const inY = Math.floor(y / 3) * 3
for (let i = inX; i < inX + 3; i++) {
for (let j = inY; j < inY + 3; j++) {
if (board[i][j] === num) return true
}
}
return false
};
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 51. N 皇后 (opens new window)
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:

输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
2
3
示例 2:
输入:n = 1
输出:[["Q"]]
2
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
题解:
和数独差不多,注意的是 line 42 这里直接过就好了不需要有什么判断。
判定那里注意两点
- 行只需要判断到当前行的上面一行,因为当前行之下(包括当前行)一定是空的
- 注意对角线的判断技巧
i - j === x - y || i + j === x + y
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function (n) {
const ans = []
// 初始化一个数组用来存放过程值
const board = Array.from({ length: n }, () => new Array(n).fill('.'))
const hasQ = (x, y) => {
// 判断列上和对角是否有(行肯定没有)
// 行只需要查找当前行之前的就行,因为之后的行都是空的
for (let i = 0; i < x; i++) {
for (let j = 0; j < n; j++) {
// 注意这里的对角线技巧
if (board[i][j] === "Q" &&
(j === y || i - j === x - y || i + j === x + y)) {
return true
}
}
}
return false
}
const fill = (x) => {
// 结束,将结果 board 处理后放入进 ans,能走到这一步的一定是满足条件的,否则都在line38被pass了
if (x == n) {
const arr = []
board.forEach(line => {
arr.push(line.join(''))
})
ans.push(arr)
}
// 判断当前行每个位置是否可填
for (let i = 0; i < n; i++) {
// 不可填 继续
if (hasQ(x, i)) continue
// 否则,填上
board[x][i] = "Q"
// 下一行
fill(x + 1)
board[x][i] = '.'
}
}
fill(0)
return ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 22. 括号生成 (opens new window)
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
2
示例 2:
输入:n = 1
输出:["()"]
2
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function (n) {
/**
* 假设n=2
* 什么时候可以选r?在r>l的时候 比如 ( 或者没l的时候
* 相等的时候不能选r 原来是() 再选r就变成())
* 字符串总长度n*2时候 结束
*/
const res = [];
const dfs = (l, r, str) => {
if (str.length === n * 2) {
res.push(str);
return;
}
if (r > l) {
// l只要不为0 还能选
if (l !== 0) dfs(l - 1, r, str + "(");
// 选r
dfs(l, r - 1, str + ")");
} else {
dfs(l - 1, r, str + "(");
}
};
dfs(n, n, "");
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
